안녕하세요, 끙정입니다.
오늘은 분류(Classification) 문제에서 자주 발생하는 클래스 불균형(Imbalance) 문제를 해결하는 방법 중에 하나인 오버샘플링 기법(Over Sampling Methods)에 대해서 알아보겠습니다.
오버 샘플링의 종류는 주로 SMOTE에서 뻗어나간 방식들이 많습니다. 최근에는 GAN을 활용한 오버 샘플링 기법도 많은 연구가 이루어지고 있습니다. 다만 이번 포스팅에서는 SMOTE 친구들만 다루도록 하겠습니다.
사실 오버 샘플링 외에도 언더 샘플링(Under Sampling) 기법이 있지만, 따로 다루지는 않겠습니다.
가정
오버 샘플링이 필요한 이유에 대해서 먼저 간단히 짚고 넘어가겠습니다. 일반적으로 우리는 머신러닝을 통해 분류 문제를 해결할 때, 이진 분류라고 하면 클래스(Class / Label)가 두 개가 존재합니다. 모델은 학습을 통해 데이터 x를 모델에 집어 넣게 되면 해당 데이터에 할당되는 클래스(이진 분류기 때문에 1 혹은 0) y를 뱉어내게 됩니다.
보통의 학습 데이터는 데이터의 비율이 크게 다르지 않지만, 현실 세계에서는 클래스 불균형이 매우 심합니다. 예를 들면, 공장 제조품의 불량 여부라든지, 카드고객의 사기여부라든지. 이런 경우는 수십만 건 중에 한 개의 경우가 있을까 말까한 수준입니다. 그럴 경우 모델은 적은 수의 클래스(Minoriry)의 분포를 제대로 학습하지 못하게 됩니다. 따라서 모델은 많은 수의 클래스(Majority)의 분포에 과대적합되기 마련이고, 어떤 데이터가 들어오더라도 Major Class로 분류하는 문제가 발생하죠.
그렇기 때문에 우리는 모델을 학습할 때, 이러한 클래스 불균형을 조정해줍니다. 바로 오버/언더 샘플링을 통해서 말이죠. 다만 위에서 말씀드렸다시피 대체적으로 Minority의 수가 매우 적기 때문에 언더 샘플링을 하는 경우는 많지 않습니다. 대부분 오버 샘플링을 하게 됩니다.
Random Over Sampling
랜덤 오버 샘플링은 아주 간단한 방식입니다. 기존에 존재하는 소수의 클래스(Minority)를 단순 복제하여 비율을 맞춰주는 것입니다. 단순 복제하여 분포는 변화하지 않습니다만, 숫자가 늘어나기 때문에 더 많은 가중치를 받게 되는 원리입니다.
ROS는 언뜻 보기에 단순히 같은 데이터를 복제시키는 것에 불과하니 성능이 좋지 않을 것 같지만, 실험적으로 유효할 때가 종종 있습니다. 그러나 똑같은 데이터가 증식되다보니 오버피팅의 위험이 도사리고 있습니다.

from imblearn.over_sampling import RandomOverSampler, SMOTE, BorderlineSMOTE, ADASYN
from collections import Counter
# ROS(Random Over Sampler)
ros = RandomOverSampler(random_state = 42)
X_res, y_res = ros.fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y))
print('Resampled dataset shape %s' % Counter(y_res))
SMOTE(Sythetic Minority Over-Sampling Technique)
가장 유명한 SMOTE입니다. 원리는 그다지 어렵지 않습니다. 그러나 거의 모든 오버 샘플링 기법이 이 SMOTE를 뿌리로 뻗어나갔다고 해도 과언이 아닐 정도로 많이 쓰이는 기법입니다.
SMOTE는 간단히 말해서 임의의 소수 클래스 데이터로부터 인근 소수 클래스 사이에 새로운 데이터를 생성하는 것입니다. 무슨 말인지 자세히 살펴보겠습니다. SMOTE는 먼저 임의의 소수 클래스에 해당하는 관측치 X를 잡고, 그 X로부터 가장 가까운 K개의 이웃 X(nn; Nearest Neighbors)를 찾습니다. 그리고 이 K개의 X(nn)과 X 사이에 임의의 새로운 데이터 X' 를 생성하는 것입니다. 식은 아래와 같습니다.

식만 보면 무슨 소리인가 싶겠지만, 아래 좌표와 식을 함께 보면서 해석을 해보겠습니다.
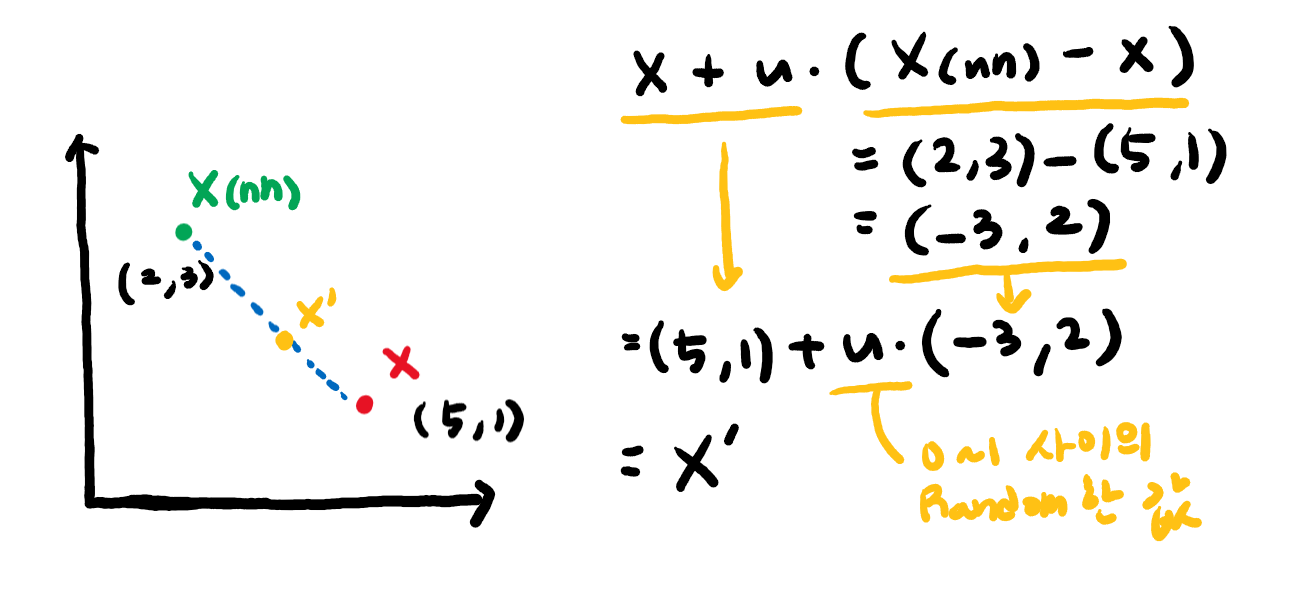
우리는 임의의 소수 클래스 관측치 X(5, 1)을 잡았습니다. 그리고 가장 근접한 이웃 K개 중에서 임의로 X(nn)(2, 3)을 잡았습니다. 우리는 여기서 (X(nn) - X)의 값에 0~1의 값을 가지는 u를 곱해서 기존의 X에 더해줍니다. 그 결과가 임의의 새로운 데이터 좌표 X' 입니다. 한마디로 X와 X(nn) 를 잇는 일직선 상에 임의의 데이터 포인트를 생성한다고 보시면 됩니다. 이 작업을 K개의 다른 X(nn)마다 진행합니다. 그 결과는 아래와 같습니다.

소수의 클래스 사이에 초록색의 새로운 데이터가 생겨난 것을 확인할 수 있습니다.
# SMOTE(Synthetic Minority Over-Sampling Technique)
smote = SMOTE(random_state = 42, k_neighbors = 5)
X_smote, y_smote = smote.fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y))
print('Resampled dataset shape %s' % Counter(y_smote))
Borderline-SMOTE
보더라인 스모트는 SMOTE에서 조금 변주를 준 알고리즘입니다. 우리는 다수 클래스(Majority)와 소수 클래스(Minority)를 구분하는 구분선을 긋고자 할 때, 가장 중요한 것은 다수 클래스와 소수 클래스가 서로 인접해 있는 경계선, 즉 Borderline의 분포가 매우 중요하다는 것을 알 수 있습니다. 그렇기 때문에 이 방식은 경계선에 있는 소수 클래스의 데이터에 대해서 SMOTE를 적용하자는 것입니다.
보더라인 스모트는 임의의 소수 클래스 데이터 X를 찾습니다. 그리고 해당 데이터 X에서 가장 근접한 K개의 데이터를 찾습니다. 근접한 K개의 클래스의 수에 따라서 [Dange, Safe, Noise] 3개로 구분을 하고 SMOTE를 실시합니다.
(1) K = K' : Noise
(2) K/2 < K' < K : Danger -> SMOTE 적용
(3) 0 <= K' <= K/2 : Safe
위의 세 경우를 살펴보면,
(1) X에 가장 근접한 K개의 클래스가 전부 Major일 경우에는 Noise로 생각하고 SMOTE를 적용하지 않습니다. 잘못된 데이터라고 생각하는 것이죠.
(3) 절반 이상이 Minor일 경우에는 Safe라고 생각하고 SMOTE를 적용하지 않습니다. 이미 X의 주변에는 Minor 데이터가 적당히 분포하고 있다는 가정이지요.
마지막으로 (2) X의 주변에 데이터 중 절반 이상이 Major일 경우에는 위험하다고 생각하고 SMOTE를 적용합니다.
즉, 완전히 홀로 고립된 데이터를 제외하고 수적 열세에 놓인 데이터의 주변에 원군을 만들어주는 것입니다. 결과는 아래와 같이 나타납니다.

# Borderline-SMOTE
bsmote = BorderlineSMOTE(random_state = 42, k_neighbors=5, m_neighbors=10)
X_bsmote, y_bsmote = bsmote.fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y))
print('Resampled dataset shape %s' % Counter(y_bsmote))
ADASYN(Adaptive Synthetic Sampling)
아다신, 에이다신 이라고도 불리는 이 방법은 보더라인 스모트에서 조금 더 변주를 준 알고리즘입니다. 기존의 보더라인 스모트가 보더라인 인근에서 [Danger, Safe, Noise] 의 3 경우로 판단해 SMOTE를 진행했다면, 아다신은 가중치를 통해 SMOTE를 적용시키는 방식입니다. 아래 표는 그 진행 방향을 잘 표현하고 있습니다.

노란 점을 임의의 소수 클래스 데이터 X라고 놓았을 때, 인근 K(K=5)개의 X(nn)을 살핍니다.
(1) 그래서 먼저 Ratio를 구합니다. Ratio는 인접한 Major 클래스를 K로 나눈 값입니다.
(2) 다음으로 스케일링을 해줍니다.
(3) 그리고 다수 클래스의 수에서 소수 클래스의 수를 빼준 값을 G라고 놓고,
(4) 스케일링 된 값에 G를 곱하면 최종적으로 생성할 샘플의 수가 나오게 됩니다.
이렇게 인접한 다수 클래스의 비율에 따라 SMOTE를 다르게 진행하게 됩니다. 결과는 아래와 같게 나타납니다.

# ADASYN(Adaptive Synthetic Sampling)
ads = ADASYN(random_state = 42, n_neighbors = 5)
X_ads, y_ads = ads.fit_resample(X, y)
print('Resampled dataset shape %s' % Counter(y))
print('Resampled dataset shape %s' % Counter(y_ads))
지금까지 총 4가지의 오버 샘플링 기법을 살펴보았습니다. 요즘에는 GAN을 활용한 오버 샘플링 기법이 많이 연구되고 있다고 들었습니다. 하지만 GAN은 딥러닝 파트로 들어가야 하기 때문에 여기서 다루지는 않겠습니다.
데이터의 분포에 따라 좋은 성능을 낼 때도 있고, 성능이 떨어질 때도 있습니다. 또한 모델링을 어떻게 하느냐에 따라서도 영향을 미칩니다. 언제나 이론은 이론이고, 실험적으로 성능을 비교해보는 것이 좋은 것 같습니다.
아래의 글과 영상을 아주 많이 참고했습니다. 감사합니다.
techblog-history-younghunjo1.tistory.com/123
[ML] Class imbalance 해결을 위한 다양한 Sampling 기법
🔉해당 포스팅에서 사용된 자료는 고려대학교 산업경영공학부 김성범교수님의 Youtube 강의자료에 기반했음을 알려드립니다. 혹여나 출처를 밝혔음에도 불구하고 저작권의 문제가 된다면 joyh9
techblog-history-younghunjo1.tistory.com
비대칭 데이터 문제 — 데이터 사이언스 스쿨
비대칭 데이터 문제 데이터 클래스 비율이 너무 차이가 나면(highly-imbalanced data) 단순히 우세한 클래스를 택하는 모형의 정확도가 높아지므로 모형의 성능판별이 어려워진다. 즉, 정확도(accuracy)
datascienceschool.net
www.youtube.com/watch?v=Vhwz228VrIk(강력 추천 드리는 김성범 교수님의 강의)
'데이터 사이언스 > 데이터 사이언스' 카테고리의 다른 글
| 범주형 변수 인코딩 방법(Categorical Feature Encoding Methods) (2) | 2021.05.14 |
|---|---|
| 지니(Gini) vs 엔트로피(Entropy) 그리고 정보 이득량(Information Gain) (0) | 2021.04.30 |
| 트리 기반 메서드(Tree Based Method) (0) | 2021.04.27 |
| 엑스트라 트리(Extra Trees) vs 랜덤 포레스트(Random Forest) (0) | 2021.04.26 |
| GBM vs XGB vs LGBM vs CATB (4) | 2021.04.25 |




댓글