안녕하세요, 끙정입니다.
오늘은 Tree Based Method에서 파티션(노드)을 분할할 때 기준으로 쓰이는 두 가지 측정방법, Gini(지니)와 Entropy(엔트로피)를 알아보겠습니다.
그리고 추가로 Information Gain(정보 이득량)을 통해서 Tree가 어떻게 Nodes를 펼쳐 나가는지 알아보겠습니다.
딥러닝에서는 크로스 엔트로피를 손실 함수로 사용하기 때문에 엔트로피는 익숙하신 분도 계실 겁니다. 지니도 엔트로피와 매우 유사하지만 조금은 헷갈립니다.
가정.
우리는 각기 다른 4개의 구슬이 담긴 3개의 주머니가 있습니다.
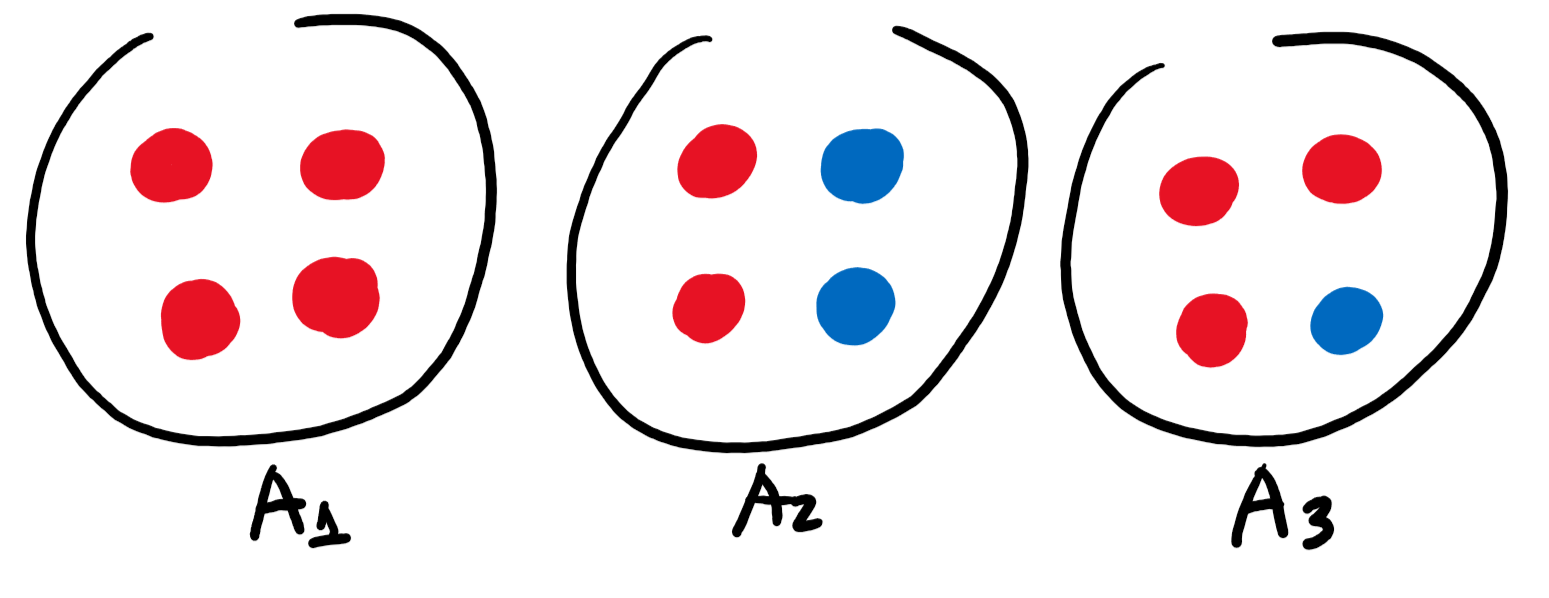
순도.
우리는 이제 기준으로 순도(Purity)를 이야기할 겁니다. 순도는 얼마나 순수한지에 대한 기준입니다. 여기서 순수의 개념은 homogeneity, 균질성입니다.
- A1은 4개의 빨간 구슬, 0개의 파란 구슬로 이루어져 있으므로 순도는 100%입니다.
- A2는 2개의 빨간 구슬, 2개의 파란 구슬로 이루어져 있으므로 순도는 0%입니다.
- A3는 3개의 빨간 구슬, 1개의 파란 구슬로 이루어져 있습니다. 이때 지니는 75%, 엔트로피는 81%의 순도를 갖습니다.
즉, 두 방법은 순도를 측정하는 기준이 다소 다름을 알 수 있습니다. 왜 그런지 수식을 통해 살펴보겠습니다.
지니.
위키피디아에서는 지니를 이렇게 정의하고 있습니다.
"measures how often a randomly chosen element from the set would be incorrectly labeled"
즉, 정답이 아닌 다른 라벨이 뽑혀 나올 확률입니다. 그렇기에 지니 인덱스는 아래와 같은 수식을 갖습니다.

구슬 주머니를 다시 계산해보겠습니다.

여기서 0의 값은 100% pure 하다는 의미입니다. 다른 주머니도 계산해볼까요?

label이 2개이기 때문에 결과를 1/2로 나누어주면 조금 더 정확한 수치가 나옵니다.

즉, 완전히 impure 한 수치가 나왔습니다. 정답 라벨과 오답 라벨이 뽑혀 나올 확률이 정확히 반반이기 때문이죠.
마지막 A3를 계산해보면 0.75, 75%가 나옵니다.

엔트로피.
엔트로피는 정보이론에서 온 개념입니다. 간단히 말해서 정보량을 의미합니다. 엔트로피가 높다는 것은 정보가 많다는 말이고, 정보가 많다는 말은 확률이 낮다는 뜻입니다. 해는 동쪽에서 뜨는 것은 100%의 확률을 갖습니다. 이 경우 엔트로피는 낮습니다. 그리고 정보가 적습니다. 반대로 해가 서쪽에서 뜨는 것은 0%의 확률입니다. 이 경우 엔트로피는 매우 높고, 정보도 매우 많습니다. 그러나 확률은 낮습니다.

수식은 아래와 같습니다.

로그를 취하기 때문에 지니 인덱스보다 연산이 무거운 것이 특징입니다. 또한 로그를 취하기 때문에 단순 확률을 사용하는 지니와 다른 값을 갖게 됩니다. 엔트로피는 로그를 취함으로써 많은 이점을 얻는다고 하는데, 자세한 사항은 여기서 다루지 않겠습니다.
구슬 주머니 계산. (2개의 label이 있기에 log base를 2로 두었습니다.)

지니와 마찬가지로 0이 나옵니다. 100% pure 합니다.

지니와 마찬가지로 1이 나옵니다. 100% impure 합니다.

지니와는 다르게 0.81이 나왔습니다. 지니보다 더 impure 하게 판단합니다.
Information Gain(정보 이득량)
우리가 앞서 순도(Purity)를 기준으로 한 이유는 바로 Information Gain을 설명하기 위함입니다. 우리는 순도를 통해 Parents Node와 Child Node에 대한 Information Gain을 산출할 수 있습니다. 그에 대한 수식은 아래와 같습니다.

Information Gain(정보 획득량)의 개념은 아주 간단합니다. Parent Node(부모 노드)의 정보량(Gini or Entropy)에서 Child Node(자식 노드)의 정보량(Gini or Entropy)을 뺀 것입니다.
우리는 앞서 정보량이 작을수록 순도가 더 높다고 했습니다. 확률도 더 높습니다. 따라서 자식 노드로 나눠질 때 정보량이 가장 작아지는 것이 좋습니다. 부모 노드에 비해 자식 노드의 정보량이 작아질수록 그 차이는 커집니다. 즉, Information Gain이 크면 클수록 순도가 더 높게 나뉘었다고 판단할 수 있습니다. ( = 더 잘 분류되도록 나뉘었다.)
그렇기 때문에 더 이상 Information Gain이 없을 때, 즉 부모 노드의 정보량과 자식 노드의 정보량의 차이가 없을 때, Tree는 분기(Split)를 멈춥니다. 정보 획득이 없기 때문입니다.
그렇다면 Gini와 Entropy로 Information Gain을 계산해보겠습니다. 아래는 간단한 예시입니다.

Gini info Gain을 살펴보면,
0.467 - {(20/35)*0.180 + (15/35)*0.391} = 0.19657
입니다.
Entropy info Gain을 살펴보면,
0.952 - {(20/35)*0.469 + (15/35)*0.837} = 0.32528
입니다.
그러나 두 방법의 범위가 다르기 때문에 더 정확한 정보 획득량을 해석하려면, 위 계산으로 획득한 정보량을 부모 노드의 정보량으로 나눠주면 됩니다.
Gini = 0.196 / 0.467 = 41.97%
Entropy = 0.325 / 0.952 = 34.14%
위 예시에서는 Gini index가 더 높은 Information Gain을 나타냈습니다.
시각화를 통한 비교.
파이썬 코드를 통해서 지니와 엔트로피 커브를 시각화해서 비교해보겠습니다. 이 시각화는 두 방법이 어떤 차이가 있는지 명확히 보여줍니다.
import random
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# Gini Function
# a and b are the quantities of each class
def gini(a, b):
a1 = (a / (a+b))**2
b1 = (b / (a+b))**2
return 1 - (a1 + b1)# Blank lists
gini_list = []
blue_list = []
red_list = []
blue_prob_list = []
# Looping Gini function on random blue and red float amounts
for x in range(10000):
blue = random.uniform(0, 4)
red = abs(4 - blue)
a = gini(red, blue)
b = blue / (blue + red)
gini_list.append(a)
blue_list.append(blue)
red_list.append(red)
blue_prob_list.append(b)
#Dataframe of amount of blue, red, Probability of blue, and gini score
df = pd.DataFrame({"Blue": blue_list,
"Red": red_list,
"Gini Score": gini_list,
"Probability of Blue": blue_prob_list})
df = df[["Red", "Blue", "Probability of Blue", "Gini Score"]]
df
plt.scatter(blue_prob_list, gini_list)
plt.xlabel("Probability of Blue Gumball %")
plt.ylabel("Gini")
plt.title("Gini Curve")
#Gini Function
#a and b are the quantities of each class. Base is the log base input.
def entropy(base,a,b):
try:
var = abs(((a)/(a+b)) * math.log(((a)/(a+b)),base)) - (((b)/(a+b)) * math.log(((b)/(a+b)),base))
return var
except (ValueError):
return 0#Blank lists
ent_list = []
blue_list = []
red_list = []
blue_prob_list2 = []
#Loop with log base 2
for x in range (10000):
blue = random.uniform(0, 4)
red = abs(4-blue)
a = entropy(2,red,blue)
b = blue/(blue+red)
ent_list.append(a)
blue_list.append(blue)
red_list.append(red)
blue_prob_list2.append(b)
df = pd.DataFrame({"Blue": blue_list, "Red": red_list,"Entropy": ent_list, "Probability of Blue": blue_prob_list})
df = df[['Red', 'Blue', 'Probability of Blue', 'Entropy']]
df
plt.scatter(blue_prob_list2, ent_list)
plt.xlabel("Probability of Blue Gumball %")
plt.ylabel("Entropy")
plt.title("Entropy Curve")
plt.scatter(blue_prob_list, gini_list)
plt.scatter(blue_prob_list2, ent_list)
plt.xlabel("Probability of Blue Gumball %")
plt.ylabel("Value")
plt.title("Both Curve")
plt.scatter(blue_prob_list, np.array(gini_list)*2)
plt.scatter(blue_prob_list2, ent_list)
plt.xlabel("Probability of Blue Gumball %")
plt.ylabel("Value")
plt.title("Both Curve")
지니 vs 엔트로피
보통의 경우 지니보다 엔트로피가 더 나은 성능을 낸다고 알려져 있습니다. 그것은 시각화를 통해 살펴본 커브를 통해 추측할 수 있습니다. 지니 인덱스 커브는 엔트로피 커브보다 경사가 더 급한 것을 알 수 있습니다. 반면에 엔트로피는 경사가 더 완만합니다. 즉, 극단값을 제외하고서는 엔트로피가 지니 인덱스보다 평가에 더 가혹하다는 것을 알 수 있습니다. 따라서 엔트로피를 기준으로 한 모델은 더 잘 분류하도록 노력합니다.
반면에 연산 속도는 지니가 엔트로피에 더 앞섭니다. 그것은 엔트로피가 로그를 사용하기 때문입니다. 이러한 속도의 차이는 데이터가 증가할수록 더 많이 벌어집니다.
따라서 시간을 투자해서라도 조금이라도 더 나은 성능을 얻고자 한다면 엔트로피를, 준수한 성능과 빠른 계산을 원한다면 지니를 사용합니다. 그러나 언제나 그렇듯이 항상 특정한 방법이 더 나은 성능을 내는 것은 아닙니다.
감사합니다.
출처.
quantdare.com/decision-trees-gini-vs-entropy/
Decision Trees: Gini vs Entropy ⋆ Quantdare
What is the difference between gini or entropy criteria when using decision trees? In this post, both of them are compared.
quantdare.com
towardsdatascience.com/gini-index-vs-information-entropy-7a7e4fed3fcb
Gini Index vs Information Entropy
Everything you need to know about impurity measurements and information gain
towardsdatascience.com
'데이터 사이언스 > 데이터 사이언스' 카테고리의 다른 글
| 범주형 변수 인코딩 방법(Categorical Feature Encoding Methods) (2) | 2021.05.14 |
|---|---|
| 오버샘플링 기법(Over Sampling Methods) (0) | 2021.05.07 |
| 트리 기반 메서드(Tree Based Method) (0) | 2021.04.27 |
| 엑스트라 트리(Extra Trees) vs 랜덤 포레스트(Random Forest) (0) | 2021.04.26 |
| GBM vs XGB vs LGBM vs CATB (4) | 2021.04.25 |




댓글